先日(10/09)に総計10個のアトラクターが見つけられれば希望があるかもと言いましたが、3時間ほど遅れて10個到達しました。
以下に順番に紹介していきます。

暫定:Twisted Attractor
二つの入力から低い方を出すmin関数(Photoshopで言う所の比較(暗))にexp関数と絶対値にしたlog関数を使用したものです。
係数を微調整していたらねじれたような形の面白いアトラクターが出来ました。ストレンジとか軌道が収束しないとかの性質はありませんが形が綺麗です。軌道のねじれなどが重なった部分に起こるモアレみたいなものが良いと思います。


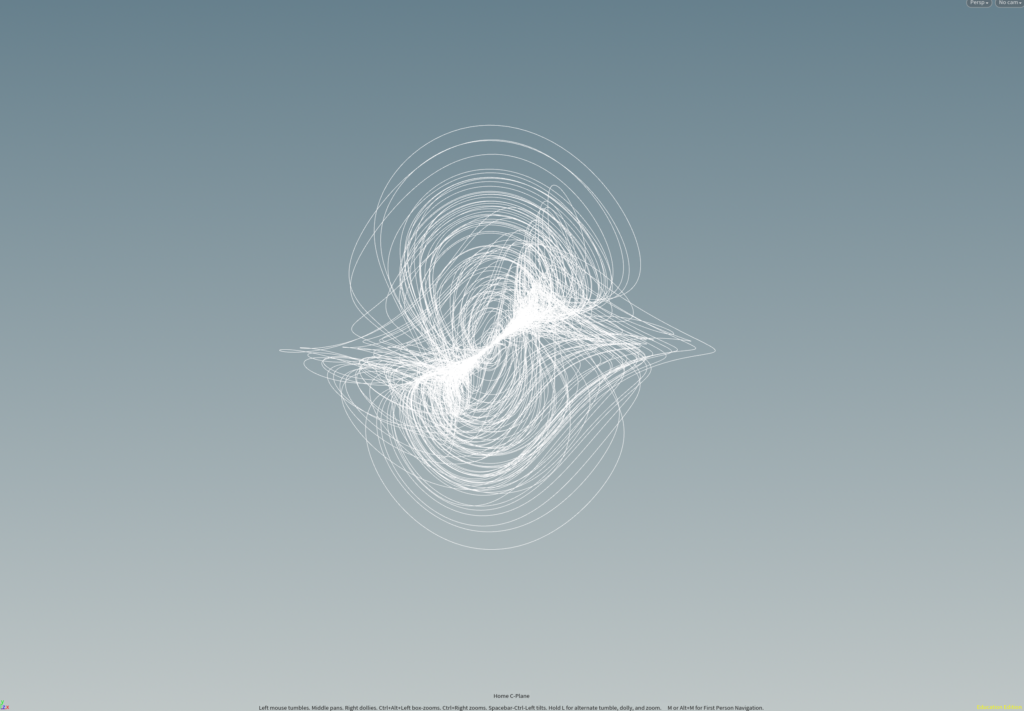
暫定:Blackhole Jet Attractor
1枚目が軌道の全体図、2枚目の白い線の太い部分が収束軌道の拡大図です。
周囲を大暴れして駆け回ったあと、内側の収束軌道に落ち着きます。とてつもなく重いブラックホールだとブラックホールの回転軸の方向にジェットが噴出されたりしているらしいのですが、この回転に対する大暴れの仕方がそれっぽいです。
内部処理には線形補間(lerp)関数を組み込んでいます。

似たような見た目のバージョン2もあります。内部処理は異なるのですが全体像はあまり違いが無いので同列に紹介します。2枚目の収束軌道が道具の持ち手のような形をしているものです。創作物にブラックホールらしき能力を持つキャラクターが登場することは多いですが、ブラックホールから噴出されるジェットを掴んで攻撃するみたいなパターンってあんまり見ないような気がします。関連性が分かりにくいからでしょうか。

暫定:Shuriken Attractor
特定の角度から見たら手裏剣みたいな形です。それだけです。こちらは内積を使っています。このあたりから総当たりで探せる限界が来ていました。とりあえず面白い形を一個作れないかと係数を微調整して手裏剣っぽくなったので完成としました。
さて、総当たりで探すのに限界が来てしまったのでアトラクターの性質を分析する必要性が出てきました。
具体的には「式のうちの何がどうなればアトラクターらしくなるのか?」です。そこで私は以前から閲覧させてもらっていたこちらのサイト1を再度訪問して数式を観察してみました。
まず「式の中に、自身の軸ではない別の軸の座標(x座標なら y, zなど)を参照する関数が存在するとアトラクターとなりやすい」可能性を考えました。ルネ・トーマスと言う人が作成したこちらのThomas Attractor2の式を見てそう考えたものです。その仮説から見つけたアトラクターが以下のものです。

暫定:Mobius Ring Attractor
軌道がメビウスの輪のような形状になるアトラクターです。吸い込める範囲は変わらず限定的でしたが、手裏剣アトラクターと同じく内積を使用しながらも自身以外の別の軸を参照するような構成にしたところこのような形になりました。
メビウスの輪と言えばドイツのオットー・レスラーによるレスラーアトラクターもメビウスの輪の性質を持っています。あちらはいきなり上に飛ぶような軌道をしている代わりに吸い込み能力に優れているのに対し、こちらは吸い込み範囲は限定的ですが紙工作で作成可能なメビウスの輪に非常に近い形状をしているように思います。
以上の仮説ではアトラクターになりやすいかは分かりませんでした。
そこで再度アトラクターの数式を観察していたところ、ローレンツアトラクター3とNose-Hoover Attractor4、Shimizu-Morioka Attractor5、Dequan Li Attractor6などのアトラクターの共通点らしきものがあるように思い、式全体の座標の2乗の項の数をそれぞれ正と負の項を並べてみました。
| Lorenz | Nose-Hoover | Shimizu-Morioka | Dequan Li | |
| 正 | dz = xy | dy = yz | dz = x2 | dx = xz, dz = xy |
| 負 | dy = -xz | dz = y2 | dy = -xz | dy = -xz, dz = x2 |
正のものと負のものとで個数が同じになっていました。調べた7と8ころDequan Li アトラクター以外のものはローレンツアトラクターをオリジナルとして分岐したものらしく、式がこういった特徴を持っていればアトラクターになりやすいのかもしれないと考えました。そこから考えて見つけたのが以下のアトラクターです。


暫定:Shoes Sole Attractor
靴のソールの形に見えるアトラクターです。横方向に非常に長く、大周りをした後に2枚目の軌道に落ちつきます。このアトラクターを見つけた時点では2乗ではない項も正と負の数をそろえて打ち消した方がいいと思っていました。
以上です。数式や係数をいじって新しい形のアトラクターを探し当てるというものに今の今更ながらハマってしまっているようなのでもしかしたら以前面談で話した「日めくりアトラクター」も良いと思い始めてきました。365枚は難しいですが100~150枚なら・・・。
・・・と言う内容を5時50分に書き終えたところ保存機能の不具合でロールバックされてしまったので急いで書き直しました。
