ちょっと気になることがあって、昨日記事を書いた後もSAを務めてる講義の課題を自己流で再挑戦してみてました。
気になる事というのは、課題内容そのままの発想からです。
位置情報を色情報化する。
・・・ただし、位置情報をそのまま色情報化するのではなく。
位置情報を新しい位置情報へ変換する漸化式を使用し、色情報化すること。
あ、今回の記事は講義内容に全く関係ないものなので「読める人が読める」ならそれでいいです。

漸化式とは
漸化式というと難しいですが中学生でも分かるように言えば「数式で計算して出てきた答え」を再び「同じ数式の同じ入力に代入」するものです。y = 3x+2という数式があるとします。このときxはどんな値でも取ることが出来ますが、とりあえずx = 0を入れてみましょう。
するとy = 3×0 + 2なので、y = 2ですね。ここでyが答えとして出てきました。
では答えのy = 2を、もういちどxとして入力してみましょう。するとx = 2です。y = 3×2 + 2となるため、y = 8です。
再度同じことをすれば、 y = 3×8 + 2でy = 26です。次はy = 80となって、さらにy = 242にもなります。
こうやって何度も繰り返し同じ数式を使用して値の変化に注目するというのが漸化式です。大雑把な解説ですが。
そしてこの漸化式ですがわざわざ自分で発見する必要があるのかと言うと、そんなことは無く。
世の中にはいくつもの漸化式があります。
その中でも私が今回スケッチに組み込んだものを紹介します。
まずは Clifford Pickover という方の名前から名付けられた「Clifford Attractor」。
もう一方は、有名な童話に登場する妖精の名前を冠する「Tinkerbell Map」です。
Clifford Attractor
クリフォードアトラクタの出自についてはほとんど知らないので、Clifford A Pickoverという方の名前を冠しているという事だけなんですが・・・実際にどういう見た目なのかについては以下のページをご覧ください。
Clifford Attractors
これらの模様はすべて極小の点群が重なって繋がって見えています。「線分は点の集合として定義される」というのもこれを見ると説得力が増すような気もします。もっともこれは曲線ですけど。非ユークリッド空間なら線分の定義は拡張されますし、それにクリフォードアトラクタはどっからどう見たって非線形ですし。sin()とcos()がこんなに関わっているので当たり前。
で。クリフォードアトラクタは以下の連立漸化式によって作られます。nxはnext xのことです。nyも同じ。nx = sin(ay) + c × cos(ax) ny = sin(bx) + d × cos(by)
この式に好きなパラメータとしてa, b, c, dを入れると、それに応じて上のページの模様が様々に描かれます。
ところで・・・考えてみてください。
このクリフォードアトラクタはx, yと二つの座標で表現されています。
対して色の情報はどうでしょう。r, g, bと3つの情報があります。言い換えれば、3つの座標を持っている・・・と言う風にも言えます。つまり、色の情報は3次元の位置情報であるとも言えるのです。
そうであるならば、3色のうち2色を使用することでクリフォードアトラクタの点群の動きを「ピクセルの色彩」として取り出せるかもしれないということが考えられます。
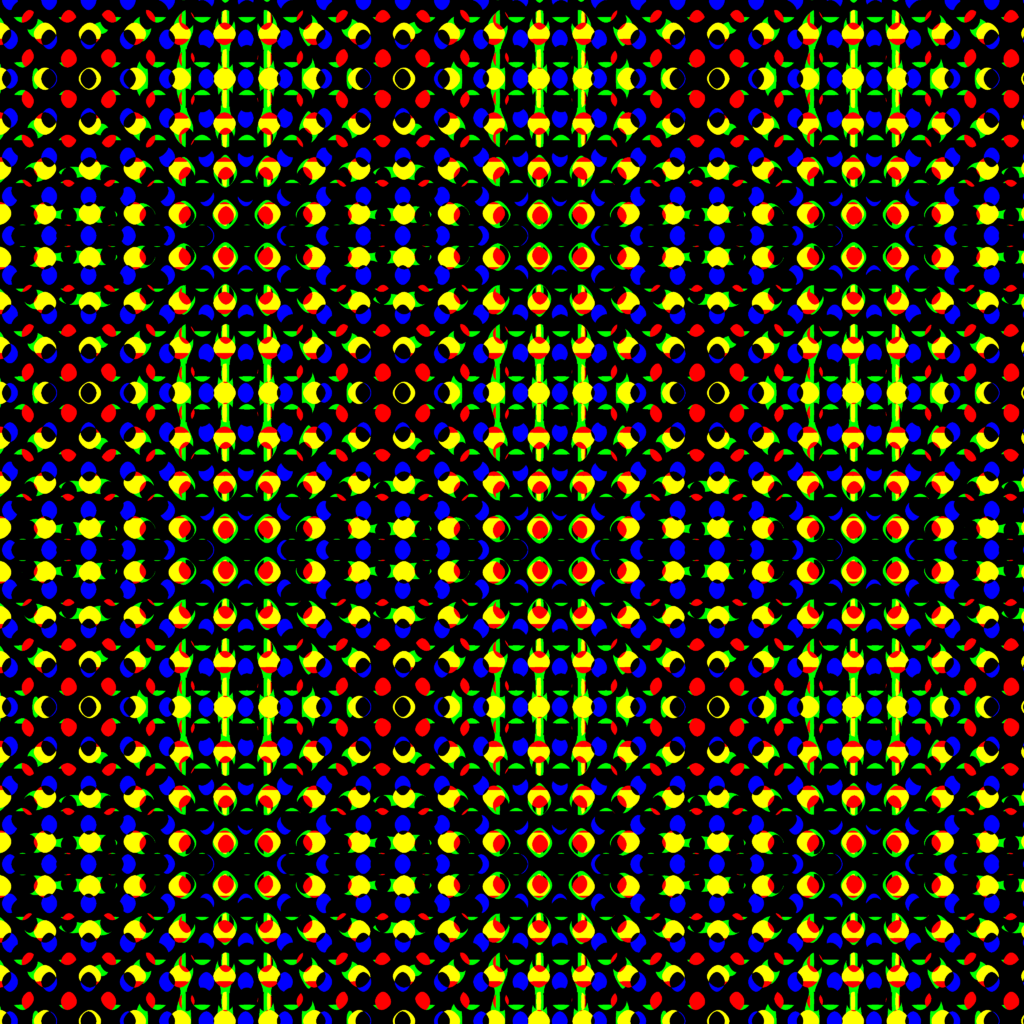
考えられたのですから、やってみましょう。それがこちら。
なんじゃあこりゃあ!!!!
・・・って心の中で思いました。いやぁ・・・すごいきれい。あからさまに脳がバグりそうな目に悪い画像ですが。
特に3枚目は異色の画面になってますね。なんでしょうこの・・・体育の授業でやってた「ブリッジ」をやってる人みたいな・・・分かりますかね。
とはいえ後から気が付きましたが、この時点でもプログラムに誤りが。
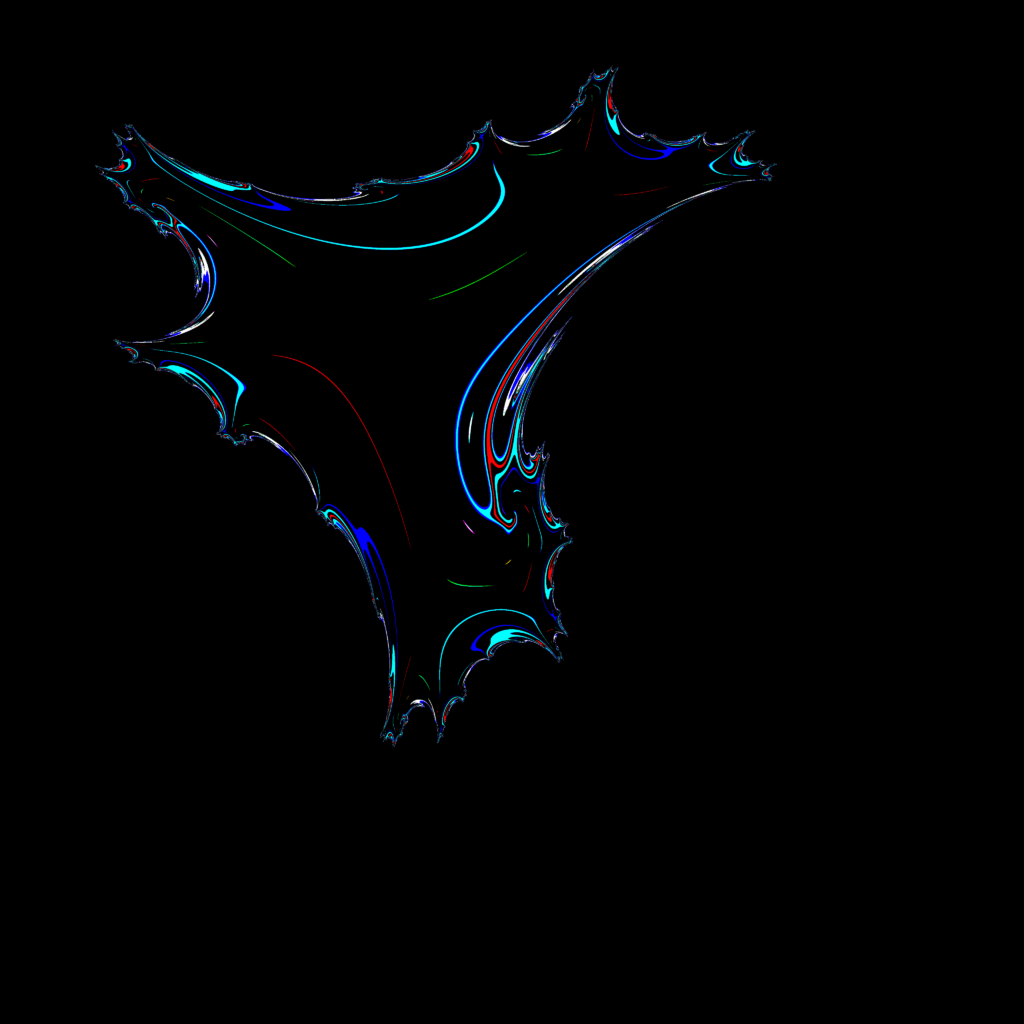
それを修正し、適切に漸化式を実行させたものがこちら。
どんどん複雑になっていきますね。マザー2のギーグみたいでちょっと気持ち悪いですけども。
しかし2枚目と3枚目の関係性はとても分かりやすいのではないでしょうか。これはおそらくカオスの性質が表面化した結果です。
最初は近距離のピクセル同士で誤差は少なく、お互いに同じ色をしていたはずですが、4回、10回を超えてくるとその近距離同士でも全く違う色を描画し始めています。
これは初期値鋭敏性というものです。たった1ピクセル、それどころか0.0000001よりも小さいわずかなズレであっても、そのズレが漸化式を実行させていく上で拡大していくのです。
クリフォードアトラクタは点群として描写されると美しくなることで知られている模様です。
また現在のところ発想の種のレベルではあるのですが、クリフォードアトラクタが描く点群の模様はもしかしたら斬撃のVFXとして使用することもできるのでは?とは考えています。一部分を切り取ってVFXとして使用したらこれまた綺麗になりそうな気がするんです。さらに点群ならHoudiniのPOP Solverで取り扱えます。漸化式をあらかじめ進行・生成させておいたポイントをPOP Sourceとして取り込む感じですかね~。みたいな妄想・構想。
Clifford Attractorについては以上。
Tinkerbell Map
またの名を「ティンカーベル写像」。写像って何ですか?と現フランス在住の方が以前おっしゃってましたが、写像について大雑把に解説を。
ざっくりいうと、写像とは関数のことです。関数と言うのはf(x) = 2xみたいなモノ。左のf(x)は、右の= 2xのxの部分に好きな数字を入れていいという意味です。
例えばf(x) → f(3)として関数fに3を入れると、関数の中で2×3が計算されます。答えは6です。
以上の流れをまとめると、関数fに好きな数値を入れると、関数の中の数式から答えが何かに決まる。
これが関数というものです。
さて、じゃあなんで写像は関数って言わないのかと言えば、写像が扱われるメインテリトリーは「集合」が関係する話だからです。関数はいろんな場所で出てきますが、集合の話で取り扱われる「関数」に関しては特に「写像」と呼ばれるみたいな理解で大丈夫だと思います。数学者が聞いたらモゾモゾして仕方がないでしょうけど。
特に写像には単射や全射といった、「入力した数値」と「返ってきた答え」を異なる2つの集合として考えることで、
「この2つの集合同士の対応関係」を観察・分析するような目的が強いように思えます。
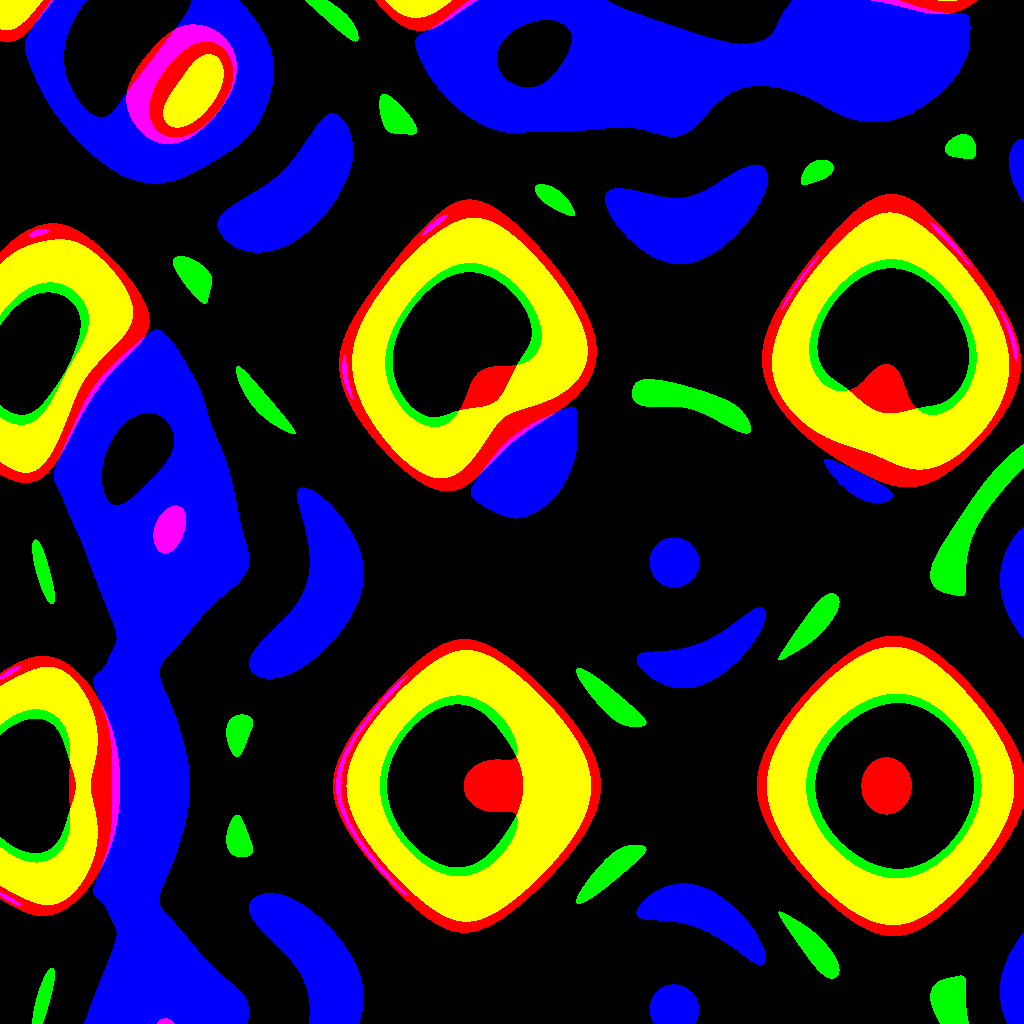
と難しい話はここまでにして、実際に見てみましょう。今度はプログラムの誤りを修正した方からみせますね。
こんな感じ。画面のちょうど中心が座標(0, 0)ですので、原点です。画像だけでなく動画でも見てみてください。
こんな感じの動き。どんどん収束しながらも初期値鋭敏性から色がバラバラに分かれていってます。
ティンカーべル写像は以下の式によって生成されます。nx = x2 + y2 + ax + byny = 2xy + cx + dy
変数a, b, c, dはクリフォードアトラクタと同じく好きなように設定できます。x, yは計算後の値が再び代入されます。
原点周囲をぐるぐる回って引き込まれて行ってる理由は良く分かりません。
こうして出てきた画像は直接見るだけでもきれいではありますが、加工することでもっときれいになります。

こんな感じ。元画像を複製して、複製したものにガウスぼかしをかけ、レイヤーをスクリーンにしました。
色相・彩度の調整レイヤーで光の色を変えることも出来ます。
この画像は1280×720ですが、オリジナル画質は3840×2160、4K画質となってます。デスクトップ壁紙用です。
後で何とかして公開できればいいと思っているのですが、どこで公開するべきか。ブログだと圧縮されちゃいますし。
かといってフルサイズで載せると重いんですよ・・・4枚以上の4K画像。当たり前です。
Boothとかで100円の値段付けたら売れるんでしょうかね?
そしてプログラムに誤りがあったときのがこれ。
これもこれで綺麗ですね。1枚目の歪んだピラミッドも良い。色の変化がちょうど陰影の様です。3枚目も時計の針のような鋭い形状。
そんなところで。そろそろ長くなってきて書いてる自分も疲れてきた。
流石に記事ひとつに半日は時間かけすぎな気がする。もっと省エネで行けるといいんですけどね・・・。
まとめ
位置情報の色情報化という初回の課題。あくまで初回の課題なのでここまで要求されることはないと思います。
とはいえ漸化式の考え方自体は単純です。答えの値をもう一度同じ数式にぶち込む!それだけ。
アーティストにとっては難しい数学的なことを考えなくていいのは利点だと思います。
今回のコードは公開するかは未定。壁紙の件もまだ分からないし、動作が重いので人に渡すのは不安。
そんなところで。記事が長すぎて校正する気が起きない・・・。